baekjoon 7869. 두 원
문제 출처
ICPC > Regionals > NEERC Far-Eastern Subregional 2000 F번
풀이
제 풀이 읽기 전, 이 글을 읽어보시는걸 추천드립니다.
제 글과 같은 풀이를 설명하고 있고, 가능한 이해가 쉬운 풀이를 보는게 도움이 될 것 같아 올립니다.
고등학교 수학을 잘 배웠다면 쉽게 풀 수 있는 문제입니다.
문제에서 두 원의 중심과 반지름만 주기 때문에, 우선 두 원이 교차하는지부터 확인해야합니다.
두 원의 중심 사이의 거리를 이용해 교차하지 않거나 완전히 포함되는 경우를 제외하면, 나머지 모든 경우에서 두 원이 교차한다고 할 수 있습니다.
우선 교차하지 않거나 포함되는 경우를 구해봅시다. 만약 두 원의 중심 사이의 거리가 각 원의 반지름의 합보다 크다면, 두 원은 교차하지 않습니다.
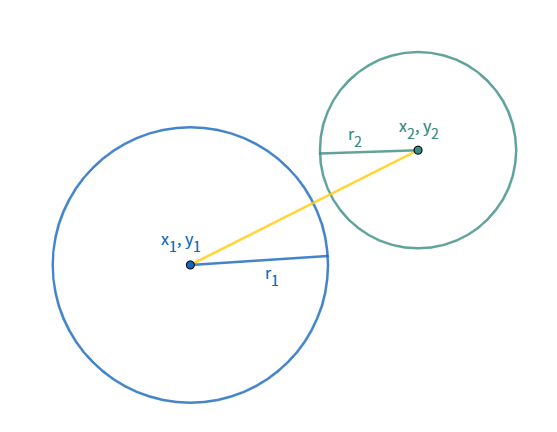
또한 두 원의 중심 사이의 거라가 두 원의 반지름의 차이 보다 작다면, 하나의 원이 다른 원 안에 완전히 포함되는 경우입니다.
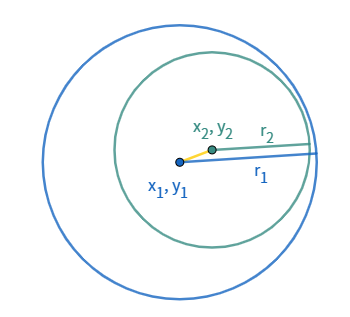
위 두 경우를 제외한 나머지 경우는 두 원이 교차한다고 볼 수 있습니다.
교차하는 넓이를 구하는 것은 (제 기억상) 고2 쯤 배웠던 것 같은 삼각함수를 사용해 구할 수 있습니다.
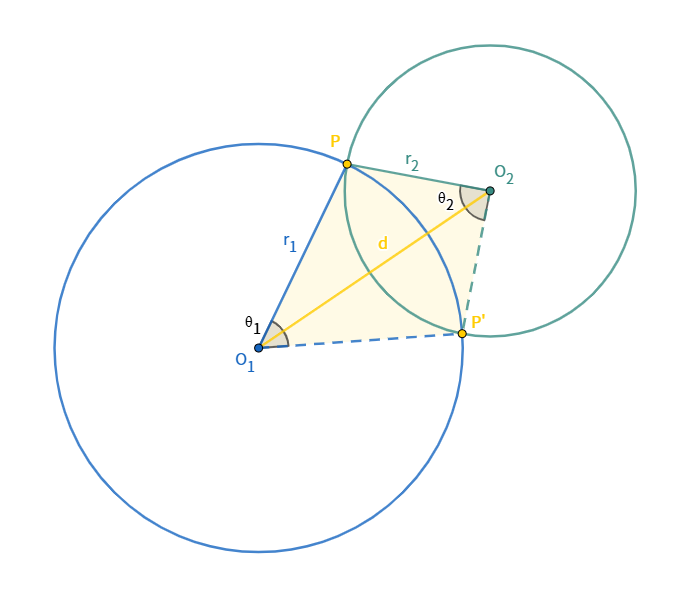
두 원의 중심을 각각 O₁, O₂라고 하고, 반지름을 r₁, r₂라고 설정해봅시다. 두 원이 교차하는 점들을 P와 P'라고 하면, 이 네 점으로 삼각형 O₁O₂P와 삼각형 O₁O₂P'를 만들 수 있습니다. 이때 선분 O₁O₂의 길이는 두 원의 중심 사이의 거리 d가 됩니다.
흥미롭게도, 이 두 삼각형은 세 변의 길이가 모두 같은 SSS 합동 삼각형입니다.
따라서 각 PO₁O₂의 크기는 전체 중심각 θ₁의 절반에 해당합니다. 이제 삼각형 O₁O₂P의 모든 변의 길이를 알고 있으므로, 코사인 제2법칙을 적용할 수 있습니다.
코사인 제2법칙에 따르면 ${r_{2}}^2 = {r_{1}}^2 + d^2 - 2r_{1}d\cdot\cos\dfrac{θ_{1}}{2}$ 라는 관계식을 얻을 수 있습니다. 이 식을 $θ_{1}$에 대해 정리하면, 코사인의 역함수를 이용하여 $θ_{1} = 2\cos^{-1}\left(\dfrac{d^2 + {r_{1}}^2 - {r_{2}}^2}{2d\cdot r_{1}}\right)$라는 공식을 도출할 수 있습니다.
마찬가지 방법으로 $θ_{2}$에 대해서도 $θ_{2} = 2\cos^{-1}\left(\dfrac{d^2 + {r_{2}}^2 - {r_{1}}^2}{2d\cdot r_{2}}\right)$라는 공식을 얻을 수 있습니다.
\[{r_{2}}^2 = {r_{1}}^2 + d^2 - 2r_{1}d\cdot\cos\dfrac{θ_{1}}{2}\] \[θ_{1} = 2\cos^{-1}\left(\dfrac{d^2 + {r_{1}}^2 - {r_{2}}^2}{2d\cdot r_{1}}\right) \quad \quad θ_{2} = 2\cos^{-1}\left(\dfrac{d^2 + {r_{2}}^2 - {r_{1}}^2}{2d\cdot r_{2}}\right)\]이제 두 부채꼴의 중심각을 모두 구했으므로, 반지름과 중심각을 이용하여 필요한 넓이들을 계산할 수 있습니다.
교차 영역의 넓이를 구하기 위해서는 두 개의 부채꼴 넓이의 합에서 두 개의 삼각형 넓이의 합을 빼야 합니다.
부채꼴 넓이의 합 $S_{1}$은 $\dfrac{1}{2} {r_{1}}^2 \theta_1 + \dfrac{1}{2} {r_{2}}^2 \theta_2$가 되고, 삼각형 넓이의 합 $S_{2}$는 $\dfrac{1}{2} {r_{1}}^2 \sin\theta_1 + \dfrac{1}{2} {r_{2}}^2 \sin\theta_2$가 됩니다. 최종적으로 구하고자 하는 교차 영역의 넓이 $S$는 $S_{1}$에서 $S_{2}$를 뺀 값입니다.
\[S_{1} = \dfrac{1}{2} {r_{1}}^2 \theta_1 + \dfrac{1}{2} {r_{2}}^2 \theta_2 \quad \quad S_{2} = \dfrac{1}{2} {r_{1}}^2 \sin\theta_1 + \dfrac{1}{2} {r_{2}}^2 \sin\theta_2\] \[S = S_{1} - S_{2} = \dfrac{1}{2} {r_{1}}^2 \theta_1 + \dfrac{1}{2} {r_{2}}^2 \theta_2 - \dfrac{1}{2} {r_{1}}^2 \sin\theta_1 + \dfrac{1}{2} {r_{2}}^2 \sin\theta_2\]이를 정리하면 $S = \dfrac{1}{2} {r_{1}}^2 \left( \theta_1 - \sin\theta_1 \right) + \dfrac{1}{2} {r_{2}}^2 \left( \theta_2 - \sin\theta_2 \right) $ 라는 깔끔한 공식을 얻을 수 있습니다.
구한 공식을 구현하기만 하면 문제를 해결할 수 있습니다.
전체 코드
#include <iostream>
#include <cmath>
using namespace std;
const double PI = acos(-1);
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
double x1, y1, r1, x2, y2, r2;
cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;
double dx = x1 - x2;
double dy = y1 - y2;
double d = sqrt(dx*dx + dy*dy);
double S;
if(d >= r1 + r2) S = 0;
else if(d <= abs(r1 - r2)) S = PI * pow(min(r1, r2), 2);
else {
double angle1 = 2 * acos((r1*r1 + d*d - r2*r2) / (2*r1*d));
double angle2 = 2 * acos((r2*r2 + d*d - r1*r1) / (2*r2*d));
double area1 = 0.5 * r1*r1 * (angle1 - sin(angle1));
double area2 = 0.5 * r2*r2 * (angle2 - sin(angle2));
S = area1 + area2;
}
cout.precision(3);
cout << fixed << S << '\n';
return 0;
}

Comments