baekjoon 16192. Voronoi Diagram Returns

Voronoi Diagram Returns

문제 출처

2018 KAIST 8th ACM-ICPC Mock Competition L번

문제 번역

다음은 제가 임의로 번역한 내용입니다.

문제

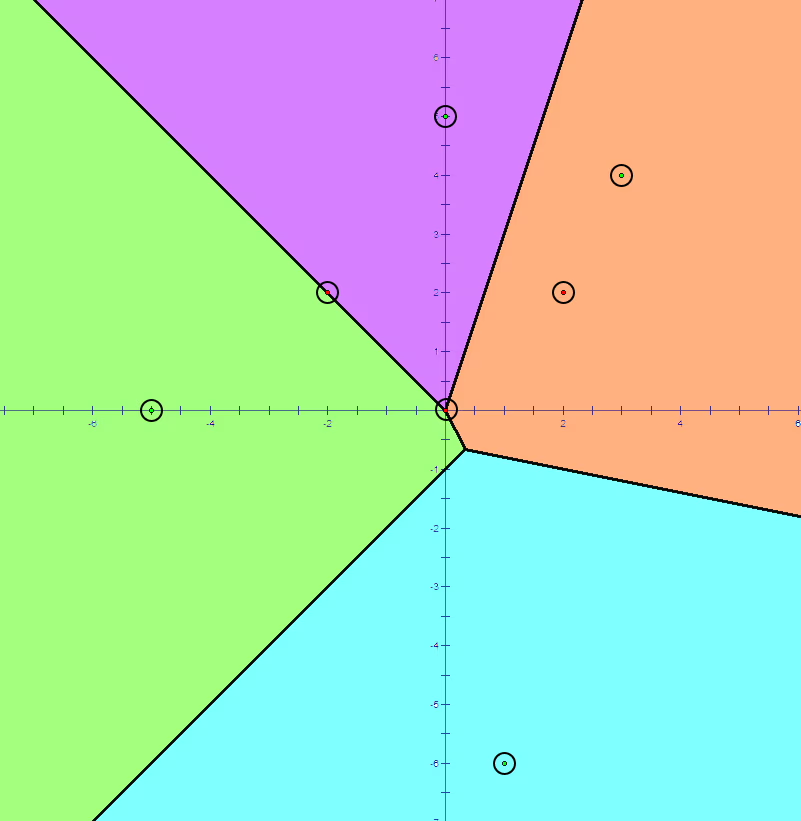
그림: 크기 4의 보로노이 다이어그램.

2차원 직교 좌표계에서, 비어 있지 않은 점의 집합 $S$에 대한 보로노이 다이어그램(Voronoi Diagram)은 평면을 “이 위치에서 가장 가까운 점이 무엇인가?”라는 기준으로 나눈 도형이다.

좀 더 정확히 말하면, 점의 집합 ${P_1, P_2, \cdots, P_n}$에 대한 보로노이 다이어그램은 여러 개의 영역으로 나뉘며, 임의의 점 $K$가 $i$번 영역에 속한다는 것은 다음 조건을 만족할 때이다.

모든 $1 \le j \le n$에 대하여, 점 $K$와 $P_i$ 사이의 유클리드 거리가 점 $K$와 $P_j$ 사이의 거리보다 작거나 같아야 한다. 즉, $d(P_i, K) \le d(P_j, K)$이다.

여기서 $d(X, Y)$는 점 $X$와 점 $Y$ 사이의 유클리드 거리이다.

예를 들어, 위 그림에서는 평면상의 모든 위치가 가장 가까운 점에 따라 색칠되어 있다.
하나의 영역에만 속하는 점은 밝은 색으로, 두 개 이상의 영역에 동시에 속하는 점은 검은 선이나 점으로 나타난다.

$\mathcal{O}(n \log n)$ 시간에 보로노이 다이어그램을 구성하는 알고리즘이 존재하지만, 이 알고리즘은 구현이 복잡하고 어렵기로 유명하다.
하지만 우리는 너그러운 출제자이므로, $n \le 2000$만 주어지며, 이는 더 느린 알고리즘을 사용해도 문제를 해결할 수 있다는 것을 의미한다.

이 문제에서는 보로노이 다이어그램 위에서 주어진 쿼리의 점이 어느 영역에 속하는지를 판단하는 점 쿼리 문제를 해결해야 한다.
점의 집합 ${P_1, P_2, \cdots, P_n}$으로 구성된 보로노이 다이어그램과 $q$개의 점 쿼리가 주어질 때, 각 점 쿼리 에 대해 다음 중 어디에 속하는지를 판별해야 한다:

• 어떤 영역에도 속하지 않으면 NONE을 출력한다.
• 정확히 하나의 영역에만 속하면 REGION X를 출력한다. 여기서 $X$는 해당 영역의 인덱스이다.
• 정확히 두 개의 영역에 속하면 LINE X Y를 출력한다. 여기서 $X$와 $Y$는 해당 두 영역의 인덱스이며, $X < Y$를 만족해야 한다.
• 세 개 이상의 영역에 속하면 POINT를 출력한다.

입력

첫째 줄에 보로노이 다이어그램을 구성하는 점의 개수 $n$과 쿼리의 개수 $q$가 주어진다.
($3 \le n \le 2, 000,\ 1 \le q \le 250, 000$)

다음 $n$개의 줄에는 각 점 $P_i$의 $x$, $y$ 좌표가 주어진다. 이 점들은 보로노이 다이어그램을 구성하는 점들이다.
모든 점은 서로 다르다. ($|x|,\ |y| \le 10,000$)

$j$번째 줄부터, $q$개의 줄에는 각 점 쿼리 $Q_j$의 $x$, $y$ 좌표가 주어진다.
각 점 쿼리에 대해, 해당 점이 어느 보로노이 영역에 속하는지 판단해야 한다. ($|x|,\ |y| \le 10,000$)

출력

출력은 총 $q$줄로 구성된다.
$j$번째 줄에는 다음 중 하나를 출력해야 한다.

• 만약 $Q_j$가 어떤 영역에도 포함되지 않는다면, NONE을 출력한다.
• 만약 $Q_j$가 정확히 하나의 영역에 포함되어 있다면, REGION X를 출력한다. 여기서 $X$는 해당 영역의 인덱스이다.
• 만약 $Q_j$가 정확히 두 영역에 포함되어 있다면, LINE X Y를 출력한다. 여기서 $X$와 $Y(X < Y)$는 해당 두 영역의 인덱스이다.
• 만약 $Q_j$가 3개 이상의 지역에 포함되어 있는 경우 POINT를 출력한다.

풀이

보로노이 다이어그램(voronoi diagram)을 이해하고 있으면 문제를 금방 이해할 수 있습니다. voronoi diagram이란 간단하게 말하자면 평면을 특정 점까지의 거리가 가장 가까운 점의 집합으로 분할한 그림입니다. 다행히도 문제에서 설명을 쉽게 해줘서 사전지식 없이도 풀 수 있습니다.

원래라면 보로노이 다이어그램 문제대로 풀어야하지만, 이 문제는 너그러운 출제자 분들이 시간제한을 무려 10초로 만들어주셨기 때문에 쿼리당 $O(n)$에 풀 수 있습니다. 현재 점에서 가장 가까운 점들의 개수를 count하여 그 개수에 따라 문제에서 요구하는 출력을 실행하면 되는 간단한 문제입니다.

쿼리마다 보로노이 다이어그램을 구성하는 $n$개의 점을 반복문을 돌며 해당 쿼리 점에서의 유클리드 거리가 가장 작은 값을 저장하고, 인덱스를 배열에 저장합니다. 만약 유클리드 거리가 저장된 최솟값과 같다면 인덱스를 배열에 추가합니다. 이후 인덱스 배열의 크기에 따라 출력을 실행합니다.

전체 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int n, q;
    cin >> n >> q;
    vector<pair<int, int>> coordinate(n);
    for(int i = 0; i < n; i++)
        cin >> coordinate[i].first >> coordinate[i].second;

    while(q--) {
        int qx, qy;
        cin >> qx >> qy;

        int minDist = 1e9;
        vector<int> idx;

        for(int j = 0; j < n; j++) {
            int dx = qx - coordinate[j].first;
            int dy = qy - coordinate[j].second;
            int dist = dx*dx + dy*dy;

            if(dist < minDist) {
                minDist = dist;
                idx = {j};
            }
            else if(dist == minDist) idx.emplace_back(j);
        }

        if(idx.empty()) cout << "NONE" << '\n';
        else if(idx.size() == 1) cout << "REGION" << ' ' << idx[0]+1 << '\n';
        else if(idx.size() == 2) cout << "LINE" << ' ' << idx[0]+1 << ' ' << idx[1]+1 << '\n';
        else cout << "POINT" << '\n';
    }

    return 0;
}